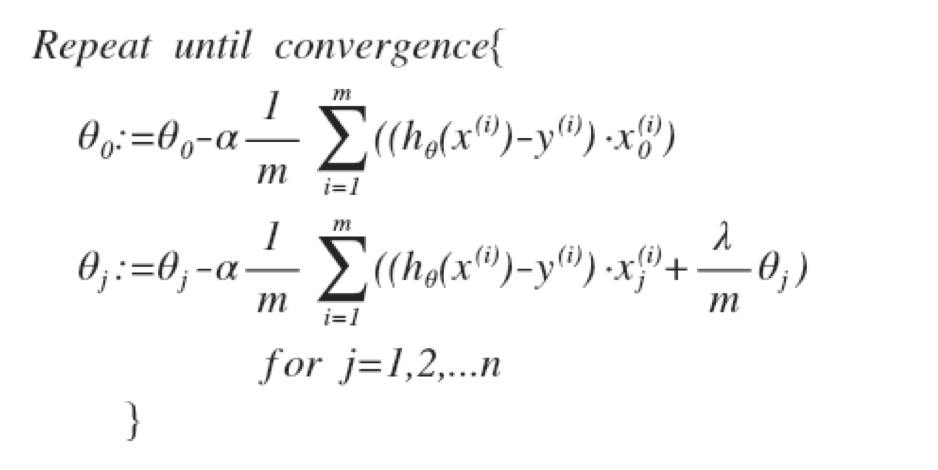机器学习 Week3 - Coursera Machine Learning

Posted on |

逻辑回归 0/1 分类问题

分类

分类问题并不是一个简单的线性问题。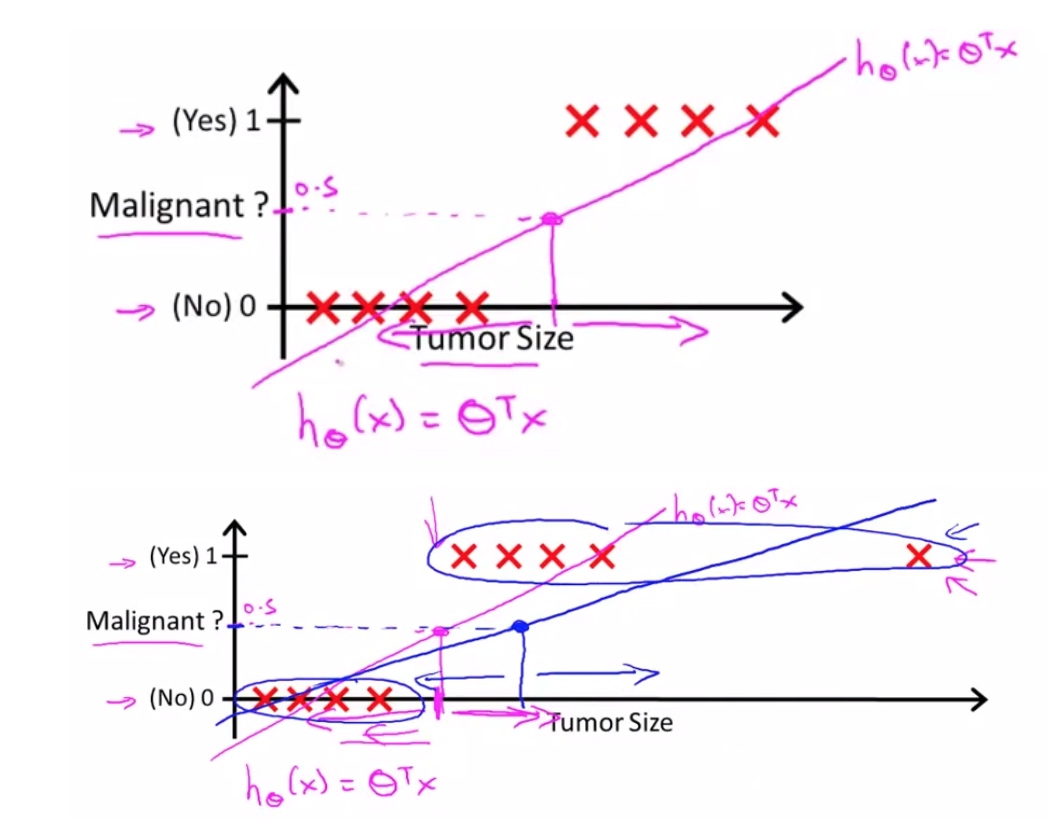

分类问题建模

人们定义了逻辑回归来完成 0/1 分类问题，逻辑一词也代表了是（1）和非（0）。

逻辑回归

目的：把预测函数限制在一个范围 $0 \leq h_\theta (x) \leq 1$

逻辑回归的假设： $h_\theta (x) = g ( \theta^T x ) $
g就是逻辑函数（sigmoid函数）$g(z) = \dfrac{1}{1 + e^{-z}}$ 下图为这个函数的图像：

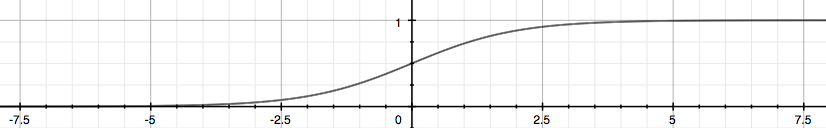
$h_\theta(x)$ 会给我们输出变量=1的概率

例子： 如果$h_\theta(x)$=0.7， 那么表示有70%的概率结果为1， 30%的概率结果为0

判定边界（DECISION BOUNDARY）

为了获得0和1，我们可以设置一个边界来判断，例如边界=0.5

根据上面绘制出的 S 形函数图像，我们知道当
$$\begin{align}z=0, e^{0}=1 \Rightarrow g(z)=1/2\newline z \to \infty, e^{-\infty} \to 0 \Rightarrow g(z)=1 \newline z \to -\infty, e^{\infty}\to \infty \Rightarrow g(z)=0 \end{align}$$

又因为 函数g的输入是 $\theta^T x$
$$\begin{align}& h_\theta(x) = g(\theta^T x) \geq 0.5 \newline& when \; \theta^T x \geq 0\end{align}$$

所以 我们可以这样作出判断
$$\begin{align}& \theta^T x \geq 0 \Rightarrow y = 1 \newline& \theta^T x < 0 \Rightarrow y = 0 \newline\end{align}$$

例子：我们知道这个是以5为边界， 小于等于5的y=1， 大于5的y=0

$$\begin{align}& \theta = \begin{bmatrix}5 \newline -1 \newline 0\end{bmatrix} \newline & y = 1 \; if \; 5 + (-1) x_1 + 0 x_2 \geq 0 \newline & 5 - x_1 \geq 0 \newline & - x_1 \geq -5 \newline& x_1 \leq 5 \newline \end{align}$$
注意的是 $\theta^T X$不一定要线性，多元方程也一样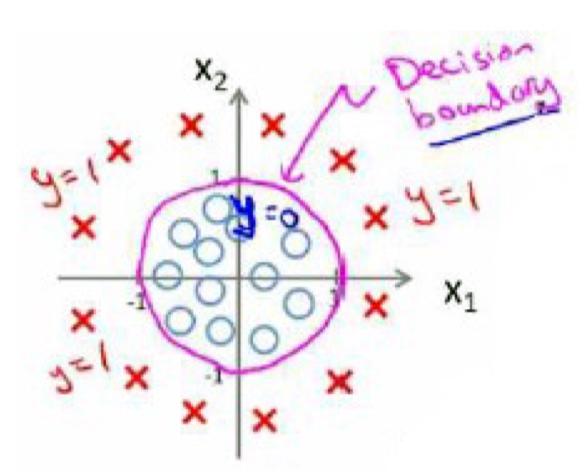

逻辑回归模型

代价函数 （Cost Function）

我们不能用线性回归的代价函数去解决逻辑回归的代价函数， 原因是我们会得到一个非凸函数（non-convex function） 这样的函数有许多局部最小值，却无法找到真正最小值。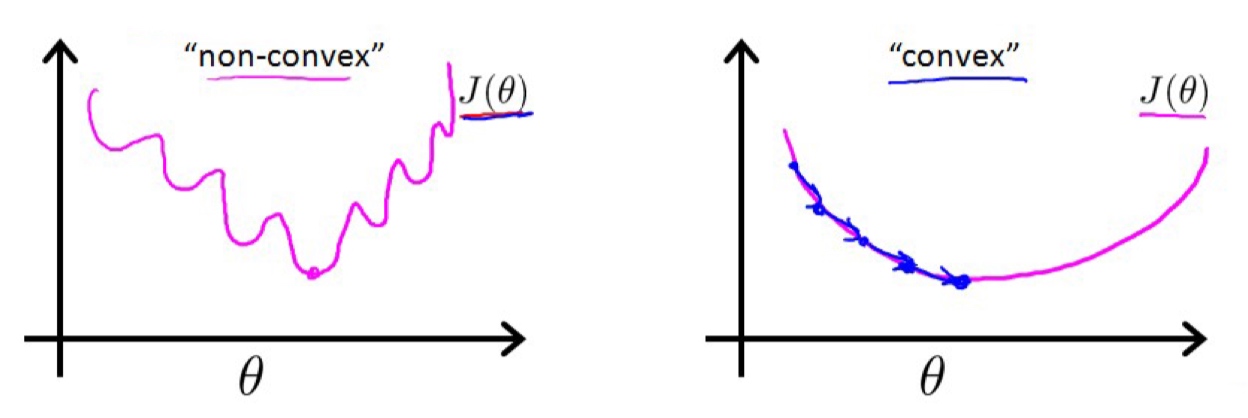

逻辑回归的代价函数
$$\begin{align}& J(\theta) = \dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)}) \newline & \mathrm{Cost}(h_\theta(x),y) = -\log(h_\theta(x)) \; & \text{if y = 1} \newline & \mathrm{Cost}(h_\theta(x),y) = -\log(1-h_\theta(x)) \; & \text{if y = 0}\end{align}$$

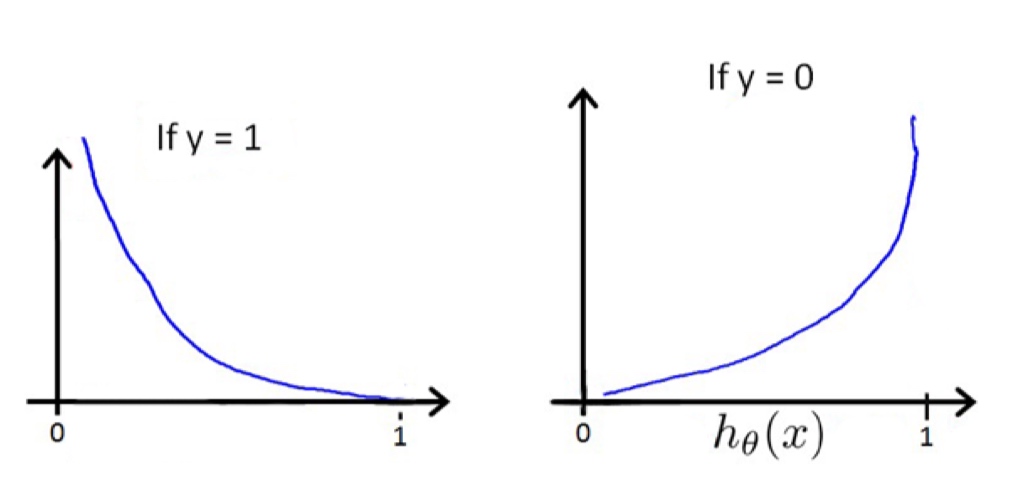
具体来说： 当y=1的时候，如果$h_\theta$也为1的时候，这样误差为0， 反之误差会趋向极限。

简化代价函数和梯度下降

代价函数也可以在一行显示：
$$\mathrm{Cost}(h_\theta(x),y) = - y \; \log(h_\theta(x)) - (1 - y) \log(1 - h_\theta(x))$$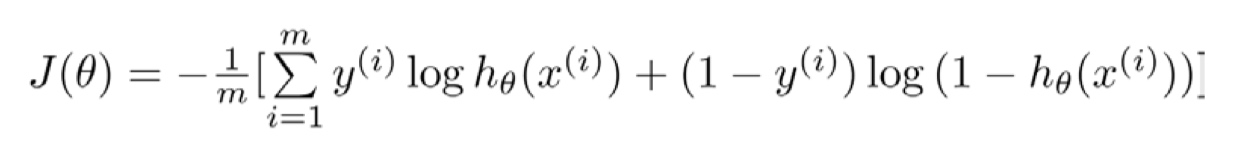

向量化：
$$\begin{align} & h = g(X\theta)\newline & J(\theta) = \frac{1}{m} \cdot \left(-y^{T}\log(h)-(1-y)^{T}\log(1-h)\right) \end{align}$$

梯度下降

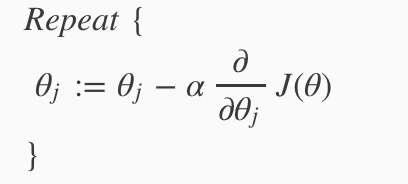
求导之后：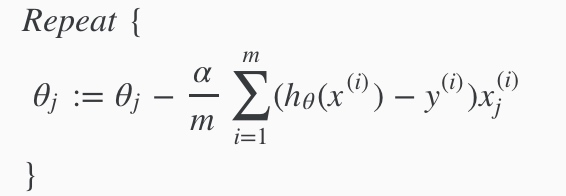

我们需要同时更新所有theta

高级优化

除了梯度下降算法以外还有一些常被用来令代价函数最小的算法，这些算法更加复杂和优越，而且通常不需要人工选择学习率，通常比梯度下降算法要更加快速。

这些算法有：共轭梯度（Conjugate Gradient）,局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)

fminunc 是 matlab 和 octave 中都带的一个最小值优化函数，使用时我们需要提供代价函数

和每个参数的求导，下面是 octave 中使用 fminunc 函数的代码示例：

1
2
3
4
5
6
7
8
function [jVal, gradient] = costFunction(theta)
  jVal = [...code to compute J(theta)...];
  gradient = [...code to compute derivative of J(theta)...];
end
options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
   [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

#多类分类（Multiclass Classification）
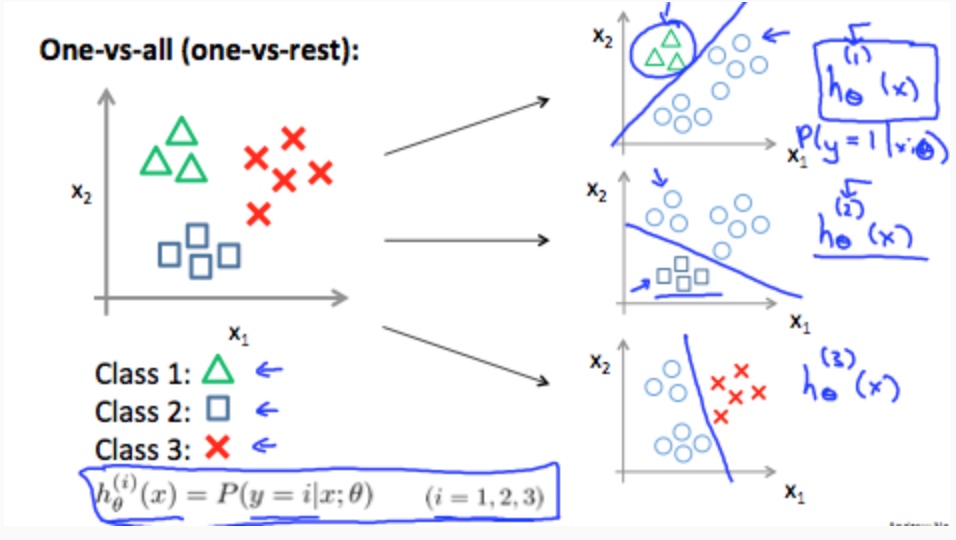
一对多 （one-vs-all）
方法是将多类分类问题转化成二元分类问题。在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量。
$\begin{align}& y \in \lbrace0, 1 … n\rbrace \newline& h_\theta^{(0)}(x) = P(y = 0 | x ; \theta) \newline& h_\theta^{(1)}(x) = P(y = 1 | x ; \theta) \newline& \cdots \newline& h_\theta^{(n)}(x) = P(y = n | x ; \theta) \newline& \mathrm{prediction} = \max_i( h_\theta ^{(i)}(x) )\newline\end{align}$

归一化 （Regularization）

过拟合 Overfitting

能非常好的拟合训练数据集， 但是不能推广到新的数据集（测试数据）

解决方法

  1. 丢弃一些特征
  2. 保留所有特征，但是减少参数的大小 （magnitude）

归一化代价函数

如果要减少一些$\theta$, 就在前面乘一个系数来进行惩罚， 以减少这些变量对最终结果的影响。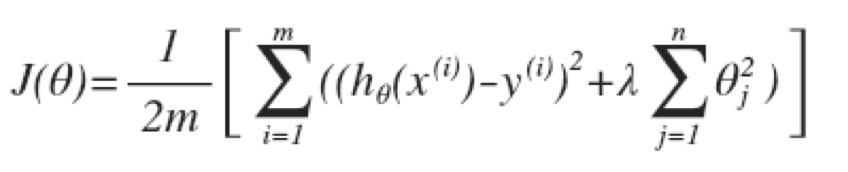

公式中的lamda呦成为归一化系数(Regularization Parameter)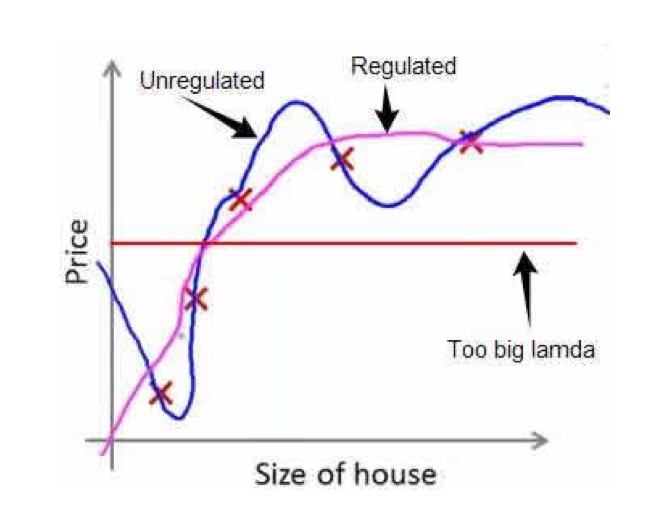

如果lamda太大， 会造成模型欠拟合

归一化线性回归 （Regularized Linear Regression）

梯度下降

我们把$\theta_0$分开，因为我们不想惩罚它。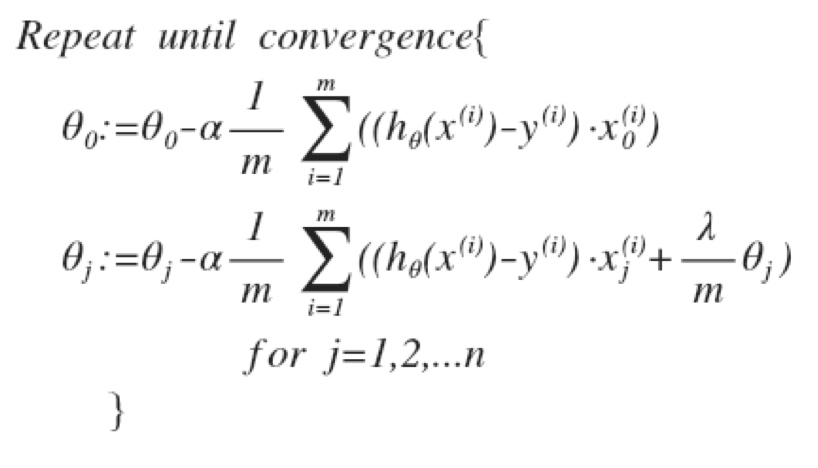

简化后：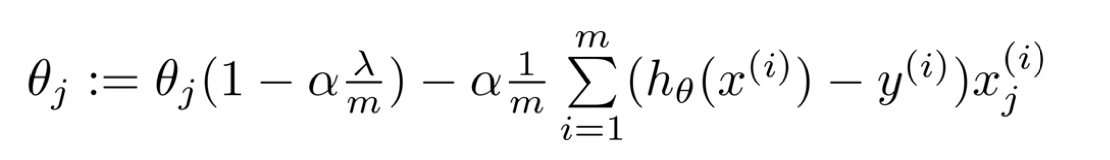

因为（1-$\alpha*lamda/m$)总是小于1， 所以每次更新都会减少$\theta_j$的值。

正规方程

和之前的正规方程不同的是， 我们加入了lamda这一项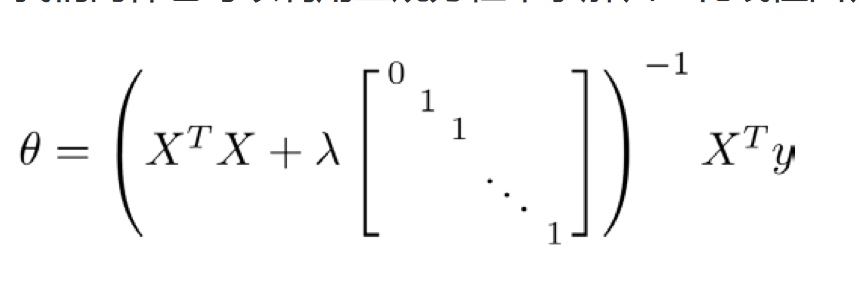

归一化逻辑回归 (Regularized Logistic Regression)

给代价函数增加一个归一化表达式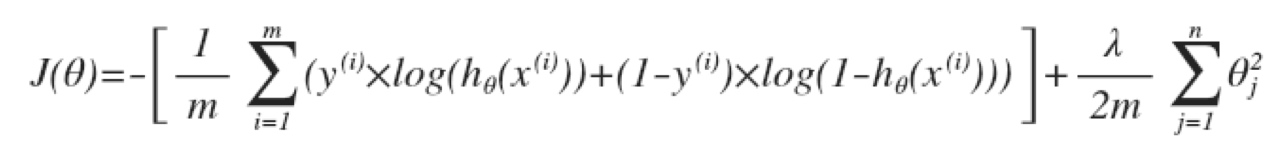

梯度下降