多元线性回归

多元特征

公式： $$h_\theta (x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 + \cdots + \theta_n x_n $$

向量化：我们可以看成矩阵相乘：

多元特征的梯度下降

和week1二元类似，也是需要同时更新所有$\theta$知道收敛
$$\begin{align}& \text{repeat until convergence:} \; \lbrace \newline \; & \theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \; & \text{for j := 0…n}\newline \rbrace\end{align}$$

梯度下降-特征缩放（Feature Scaling）

确保所有特征在一个相近的范围内，这样收敛的速度大大增加

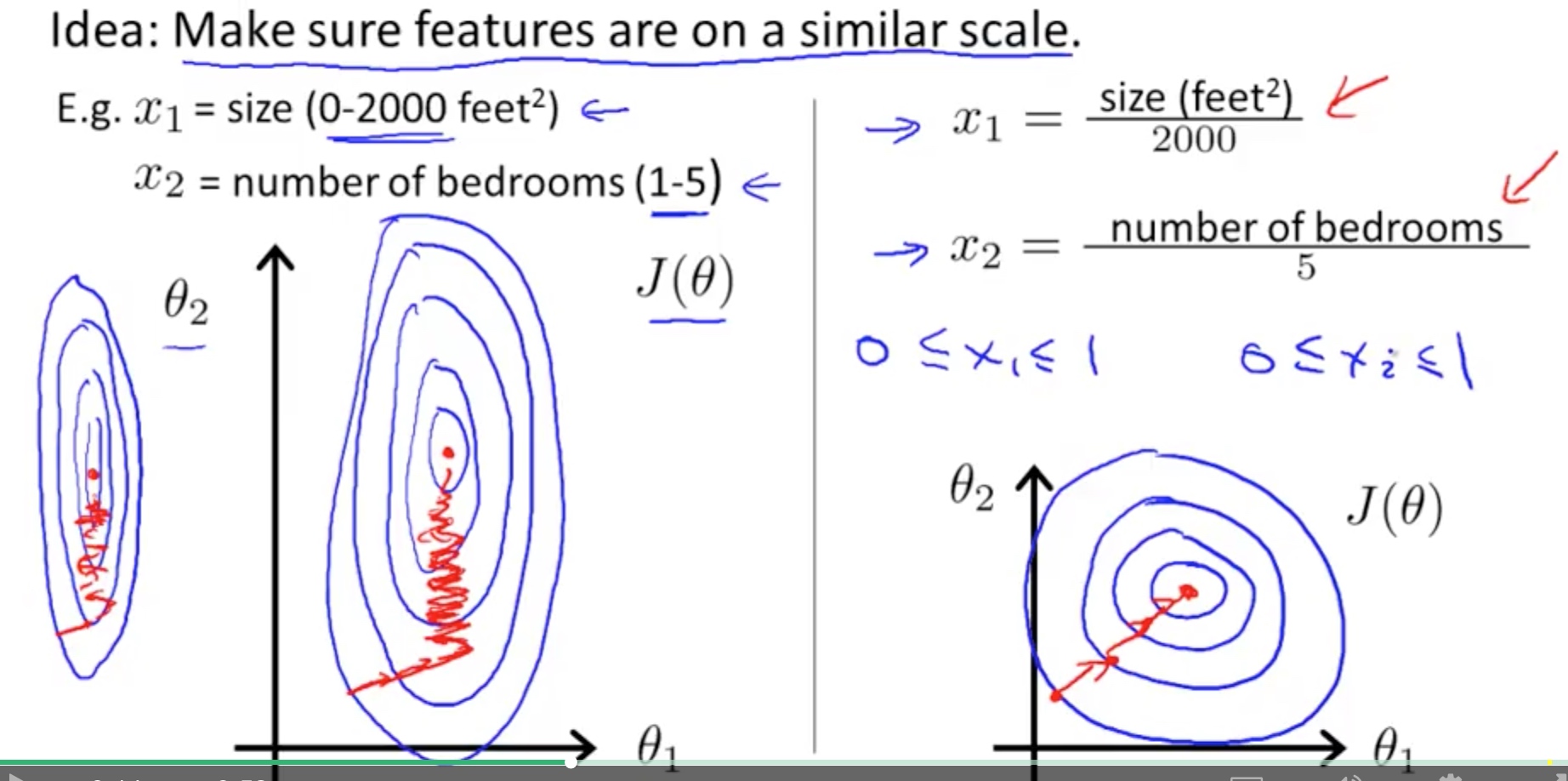
均值归一化（Mean Normalization）

$$x_i := \dfrac{x_i - \mu_i}{s_i}$$
$\mu_i$是这个特征的平均数
$s_i$是这个特征的范围（最大-最小）

例子： $x_i$表示房价范围¥100-¥2000，平均房价¥1000
$$x_i := \dfrac{price-1000}{1900}$$

梯度下降-学习速率（Learning Rate）

确保梯度下降正确

如果正确J(θ)应该一直减小

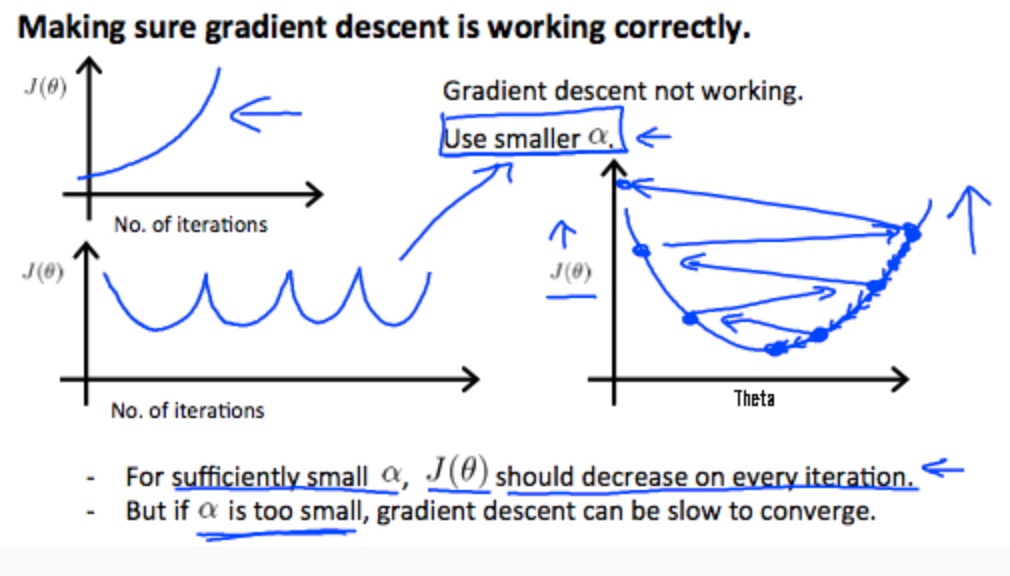
总的来说：

$\alpha$太小->收敛慢
$\alpha$太大->可能无法收敛

特征和多项式回归

我们可以把不同的特征组合起来
组合：例如把$x_1$和$x_2$乘起来组合成新特征$x_3$

多项式回归

成本函数不一定要线性，有时候二元活着三元函数更符合。
注意：多项式回归时特征缩放很关键

#计算变量

正规方程（Normal Equation）

一次性求接出最佳的$\theta$

公式： $$\theta = (X^T X)^{-1}X^T y$$
不需要做特征缩放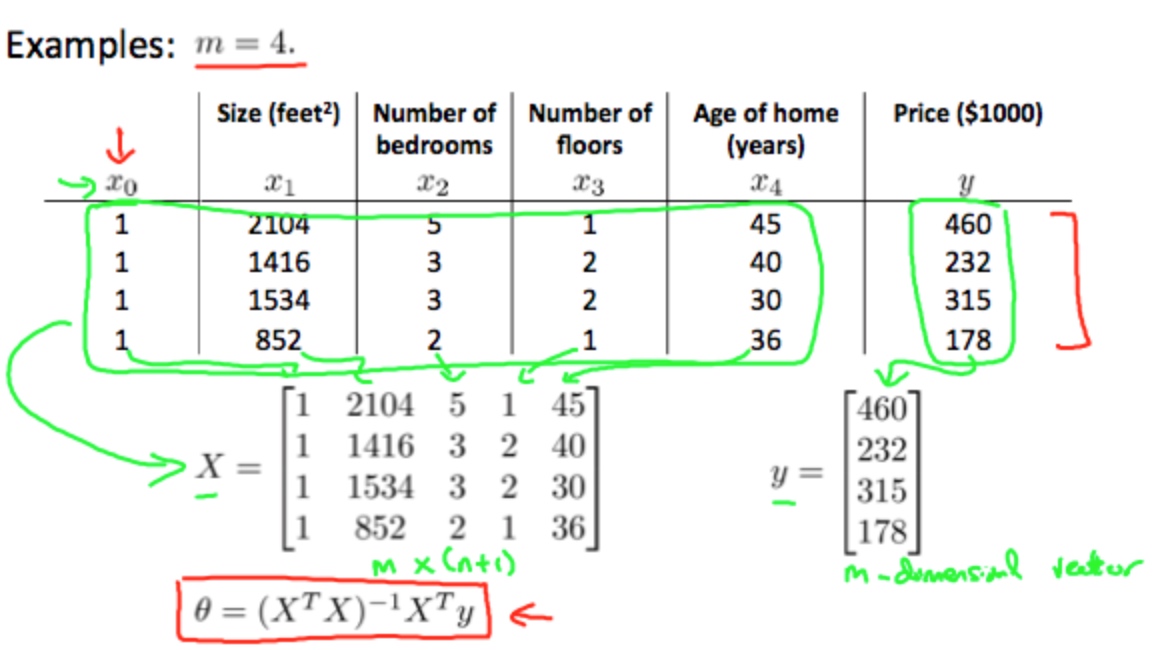

与梯度下降的区别：

梯度下降适合大数据，
正规方程适合小数据

正规方程不可逆（Normal Equation Noninvertibility）

可能的原因：

多余的变量
太多特征