介绍
什么是机器学习?
“A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.” – Tom Mitchell
一个计算机程序从一些目标(T)和结果(P)学到的经历(E)。 如果这个程序能随着经历(E)的改进而改进目标(T)的结果(P),那这就是机器学习。
举例来说: 玩跳棋
E = 多次游戏的经历
T = 玩象棋
P = 下局获胜的概率
一般来说, 任何机器学习都可以分成两类: 监督学习(Supervised Learning)和非监督学习 (Unsupervised Learning)
监督学习
我们知道正确的结果,找到输入和输出的关系
监督学习有两类。
Regression(回归问题) 主要用于预测连续变量
例子: 预测房价
Classification(分类) 主要用于预测不连续的变量
例子: 预测房价是否大于报价
非监督学习
在不知道结果的情况下解决问题。
通过变量之间的关系进行费雷
在非监督学习,我们不能得到预测结果的反馈
例子: Clustering (归类)
在一百万个基因中根据它们之间的关系或相似程度找到自动分组。
例子: Non-clustering (非归类)
鸡尾酒派对算法 - 在吵杂的环境中找到个人的声音
模型解释
我们用\(x^i\)表示输入变量, 也叫Feature。 用\(y^i\)表示输出,也就是预测结果
\((x^i,y^i)\) - 训练样本
\((x^i,y^i); i=1,…,m\); - 训练集
假设h(x)-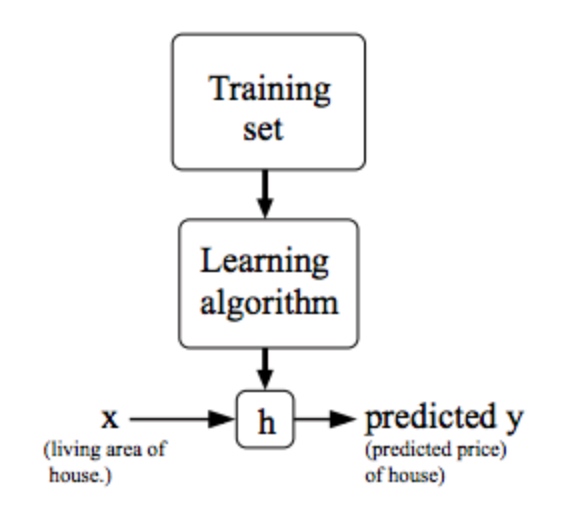
成本函数 (Cost Function)
也称作MSE(Mean Squared Error)
用来测量我们函数的正确性-最常用在回归问题上
(预测值-真实值)的平方和/(样本个数*2)
PS: 公式中除2的原因只是保证这个函数不受样本个数的影响
参数学习
梯度下降法 (Gradient Descent)
通过调整成本函数的参数来达到MSE最小
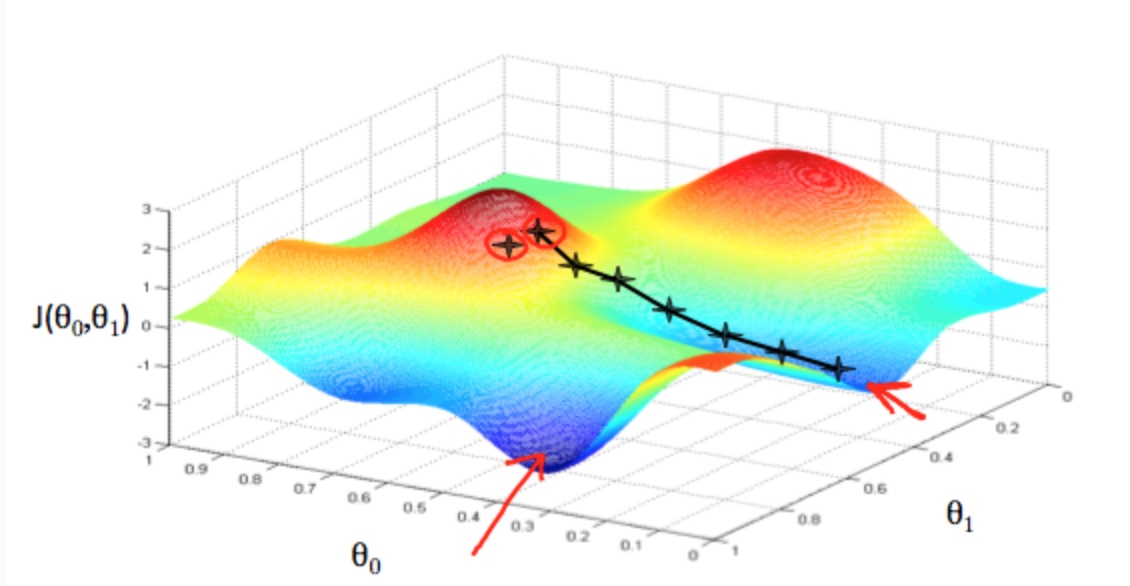
假设我们把$\theta_0$和$\theta_1$分别放在x,y轴, 然后用z轴表示我们的成本函数。
我们要做的事找到图中最低的点(红箭头)。方法是在成本函数求导数,切线的斜率提供方向,找到最陡的方向进行下降。
步子的大小叫做learning rate $\alpha$
梯度下降公式:
$$\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)$$
有多个$\theta$的时候要同时更新