第五章 预处理数据及减少范围
内容
- 完美数据-让我们现实生活中的数据趋于完美(消化missing数据)
- 基本特征选择算法
- 用PCA减少特征(Principal Components Analysis)
- 用MDS映射数据(Multi-Dimensional Scaling)
- 简单看一下处理文字数据
从数据工程师角度看
数据太少
- 难找到合理复杂度模型
- 难获得可靠数据以及统计显著性
数据太多
- 成本增加(时间与资源)
- 重复数据可能导致偏见
- 冗余数据可能导致偏见
- 多维度问题难解释和图像化
完美数据
- 可以代表
- 复杂性
- 数量和dimension
- 没有太多噪音
- 没有太多missing value
解决missing value的方法:
- 用平均数
- 用其他数据做模型
- 直接删除
基本特征选择算法
目的: 改善模型学习结果并减少学习成本
feature selection:找到最好的subset
feature reduction:找到最有效的数据组合
两者的目的都是减少原数据并保存游泳的信息
特征选择一
预测能力:
- 计算每个输入并选择最好的
- 是这把其他的输入和最好的配对,选择最好的配对
- 继续上面步骤直到获得好的结果
注意点: 要使用另外的数据做验证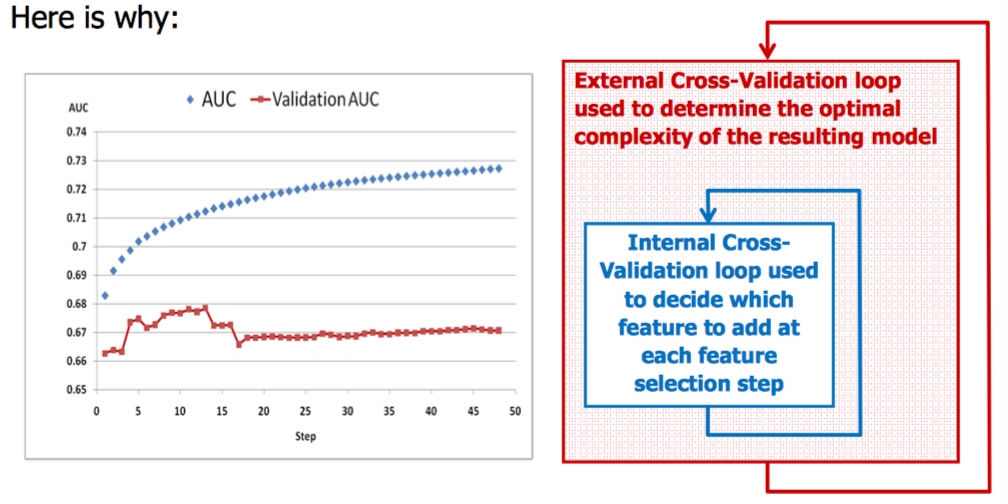
穷尽法(最优,耗时)
PCA
目的: 用不相关的数字变量替换相关的数字变量
其他目的:减少维度同时获得最大的variance
在仅仅使用有限的维度进行数据精确的翻译
PCA的原理就是将原来的样本数据投影到一个新的空间中,相当于我们在矩阵分析里面学习的将一组矩阵映射到另外的坐标系下。通过一个转换坐标,也可以理解成把一组坐标转换到另外一组坐标系下,但是在新的坐标系下,表示原来的原本不需要那么多的变量,只需要原来样本的最大的一个线性无关组的特征值对应的空间的坐标即可。
比如,原来的样本是301000000的维数,就是说我们有30个样本,每个样本有1000000个特征点,这个特征点太多了,我们需要对这些样本的特征点进行降维。那么在降维的时候会计算一个原来样本矩阵的协方差矩阵,这里就是10000001000000,当然,这个矩阵太大了,计算的时候有其他的方式进行处理,这里只是讲解基本的原理,然后通过这个10000001000000的协方差矩阵计算它的特征值和特征向量,最后获得具有最大特征值的特征向量构成转换矩阵。比如我们的前29个特征值已经能够占到所有特征值的99%以上,那么我们只需要提取前29个特征值对应的特征向量即可。这样就构成了一个100000029的转换矩阵,然后用原来的样本乘以这个转换矩阵,就可以得到原来的样本数据在新的特征空间的对应的坐标。301000000 100000029 = 30 29, 这样原来的训练样本每个样本的特征值的个数就降到了29个。
迷惑
另外一个迷惑,在最初刚开始做的时候,就是为什么这么大的数据,比如301000000直接就降到了3029,这不是减少的数据有点太多了么,会不会对性能造成影响。之所以有这个迷惑,是因为最初并不了解pca的工作方式。 pca并不是直接对原来的数据进行删减,而是把原来的数据映射到新的一个特征空间中继续表示,所有新的特征空间如果有29维,那么这29维足以能够表示非常非常多的数据,并没有对原来的数据进行删减,只是把原来的数据映射到新的空间中进行表示,所以你的测试样本也要同样的映射到这个空间中进行表示,这样就要求你保存住这个空间坐标转换矩阵,把测试样本同样的转换到相同的坐标空间中。
有些同学在网上发帖子问对训练样本降维以后,怎么对测试样本降维,是不是还是使用princomp这个函数进行降维,这个是错误的。如果你要保证程序运行正常,就要保证训练样本和测试样本被映射到同一个特征空间,这样才能保证数据的一致性。
variance = difference between data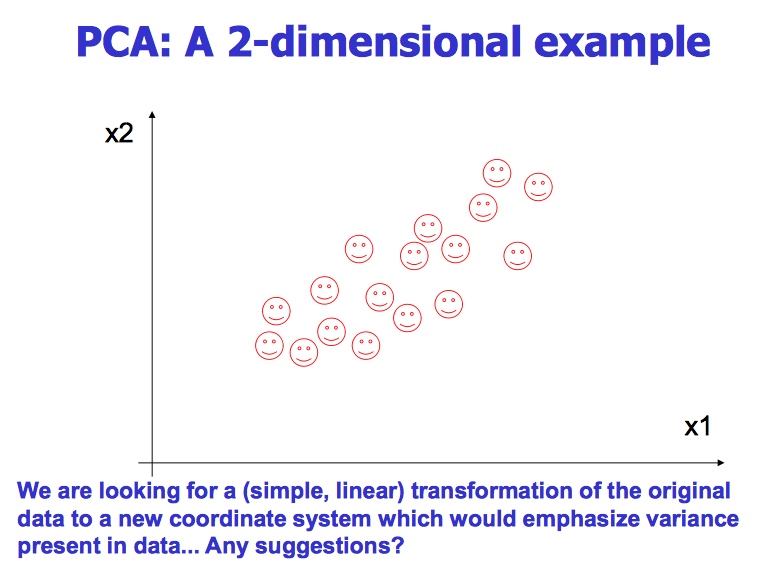
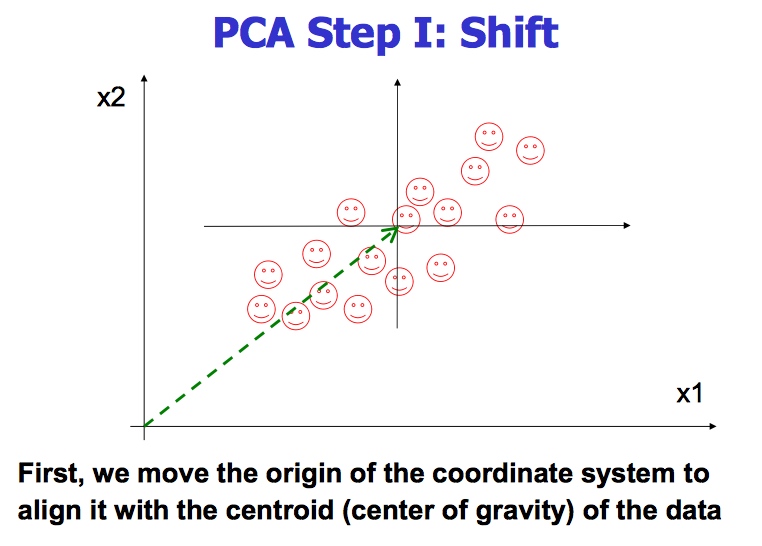
、
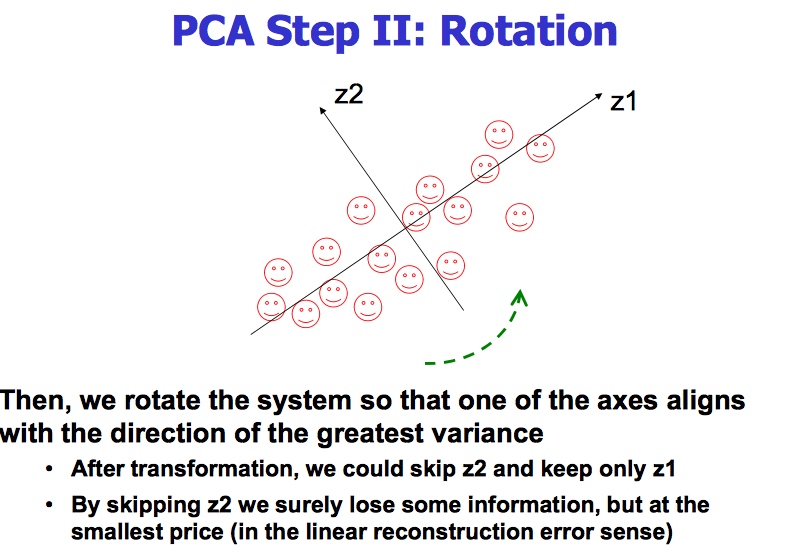
失去了一些Z2的信息
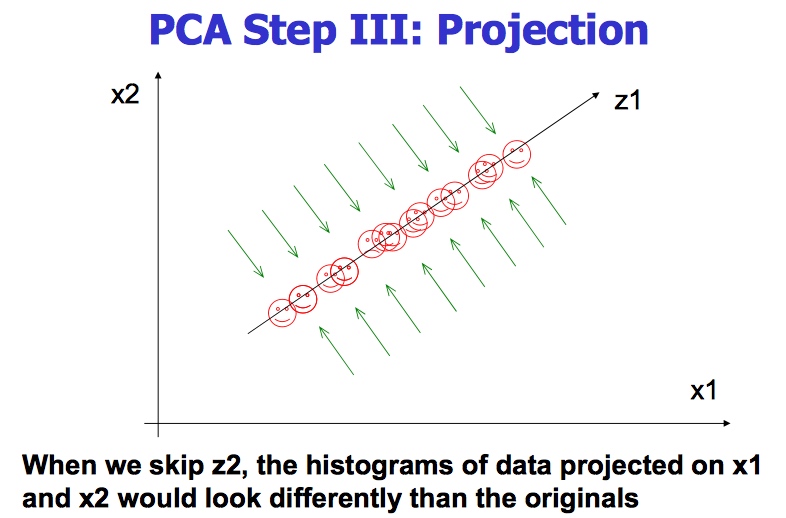
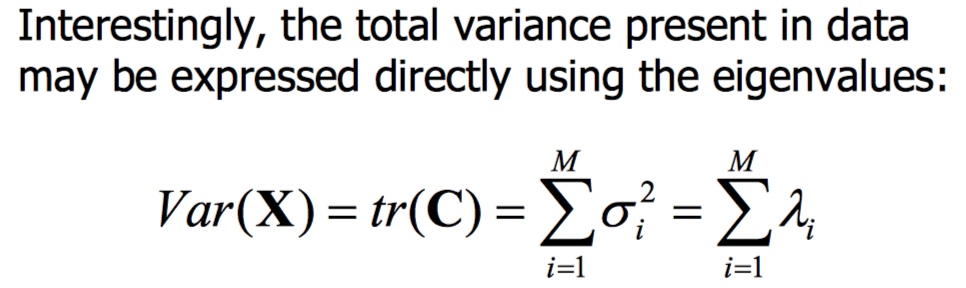

total variance = 1 + 5 + 2 = 8
1-2 are correlated
3 are not correlated
combine 1 and 2
we lose no variance
we will lose 0.17
we will lose 2.17
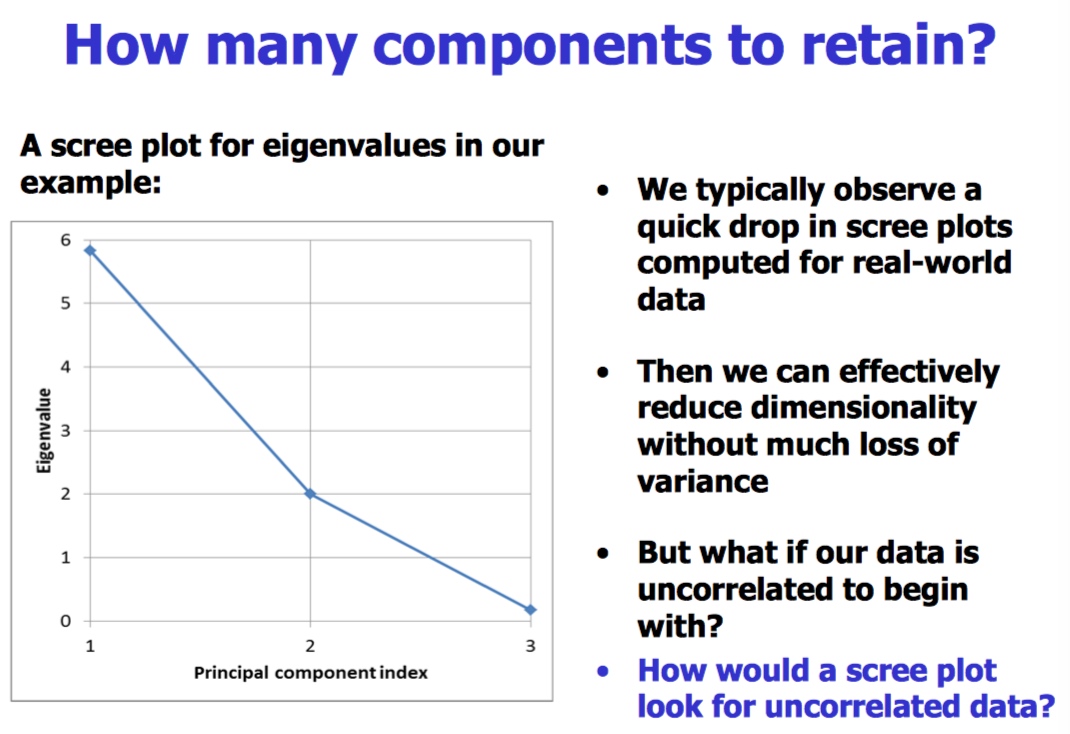
PCA总结
因为简单非常流行
通常作为数据预处理的方法
对多维度数据可视化有帮助
在图像处理和理解方面流行
本质:降低维度
不能处理qutratic value
MDS
PCA是把观察的数据用较少的维数来表达,这点上两种方法的相似的;两种方法的不太之处在于,MDS利用的是成对样本间相似性,目的是利用这个信息去构建合适的低维空间,是的样本在此空间的距离和在高维空间中的样本间的相似性尽可能的保持一致。PCA 主要是找到最能体现数据特点的特征,而 MDS 更看重的是原始数据之间的相对关系,通过可视化的方式将他们之间的相对关系尽可能准确的展现出来。
MDS 的目的是将一组个体间的相异数据经过 MDS 转换成空间构图,且 保留原始数据的相对关系 。也就是说我们通过 MDS 可以直观的可视化的展现原始数据间的相对关系。
输入: distance matrix
返回: k维度散点图保留各个对象见的距离
数学: 最小化“stress”
MDS应用范围
市场部
政治
Text Mining
动机:超多文字data
应用:文档分类, 信心获取,情感分析
最简单的想法:文字包
存储文字和出现的次数
结构化与非结构化
文档化矩阵, 每一列代表不同的:单词,一对词,词的顺序
变量:
binary
counts
weighted frequencies
TF-IDF
tf-idf模型的主要思想是:如果词w在一篇文档d中出现的频率高,并且在其他文档中很少出现,则认为词w具有很好的区分能力,适合用来把文章d和其他文章区分开来。该模型主要包含了两个因素: